Hello, I’m happy you’re here.
Thanks for stopping by!
My area of research focuses on probabilistic machine learning, deep learning and Reinforcement Learning for solving industrial optimization problems.
This can be achieved by combining large-scale distributed optimization and a variant of deep Q-Learning. Recent algorithms support for continuous action spaces makes it suitable for robotics problems and optimal control problem in industrial applications. A model is first trained offline and then deployed and fine-tuned on the real robot.
I have worked on particular project with focus on approximate inference for neural networks and Bayesian optimization. These models allow to design algorithms that can incorporate prior knowledge, quantify uncertainty, and out-of-distribution detection for large dataset. Especially in the context of neural networks, these problems remain challenging.
BSc in Mathematics 2019, MSc in Applied Mathematics ∙ Polytechnique Montreal-University of Montreal ∙ 2021
Recent Projects…
I’ve been inspired by the increasing desire to efficiently tune machine learning hyper-parameters and make better generalization under distributional shifts. I am looking for rigorously analyse conventional and non-conventional assumptions inherent to Bayesian optimisation and approximate inference. Automating the process of choosing the best forecasting model and its corresponding parameters can result to improve a widerange of real-world applications.
Financial Time Series Forcasting with Transformser ∙ Morgan Stanley, NY, USA ∙2022
Benchmarks for Out-of-Distribution Generalization in Time Series Tasks ∙ MILA, Montreal, Canada ∙2021
Improved Deep Learning Workflows Through Hyperparameter Optimization with Oríon ∙ IBM, Canada ∙2020
Collaborating With People about Their Passion
Deep Reinforcement Learning-WindFarm
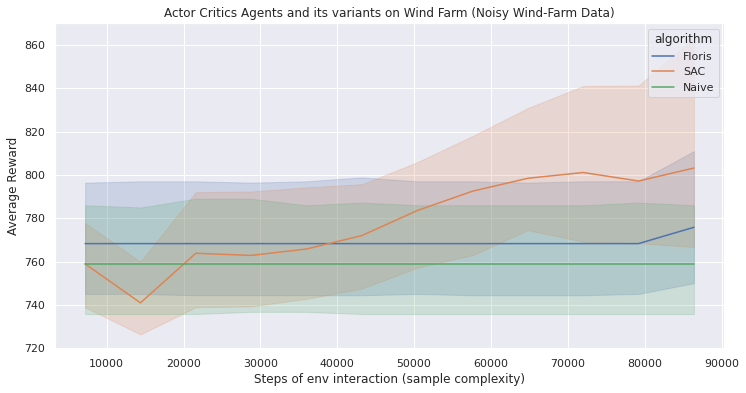
Reinforcement learning is known to be unstable or even to diverge when a nonlinear function approximator such as a neural network is used to represent the action-value known as Q function.
Projects
Neural ODE Tutorial
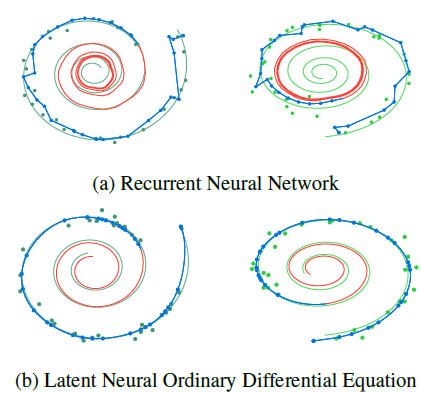
Introduction to Neural ODE The Neural Ordinary Differential Equations paper has attracted significant attention even before it was awarded one of the Best Papers of NeurIPS 2018. The paper already gives many exciting results combining these two disparate fields, but this is only the beginning: neural networks and differential equations were born to be together. This blog post, a collaboration between authors of Flux, DifferentialEquations.jl and the Neural ODEs paper, will explain why, outline current and future directions for this work, and start to give a sense of what’s possible with state-of-the-art tools.
Publications
Approximate Bayesian Optimisation for Neural Networks
A novel Bayesian Optimization method based on a linearized link-function to accounts the under-presented class by using a GP surrogate model. This method is based on Laplace’s method and Gauss-Newton approximations to the Hessian. Our method can improve generalization and be useful when validation data is unavailable (e.g., in nonstationary settings) to solve heteroscedastic behaviours. Our experiments demonstrate that our BO by Gauss-Newton approach competes favorably with state-of-the-art blackbox optimization algorithms.
Talks
Approximate Bayesian Neural Networks
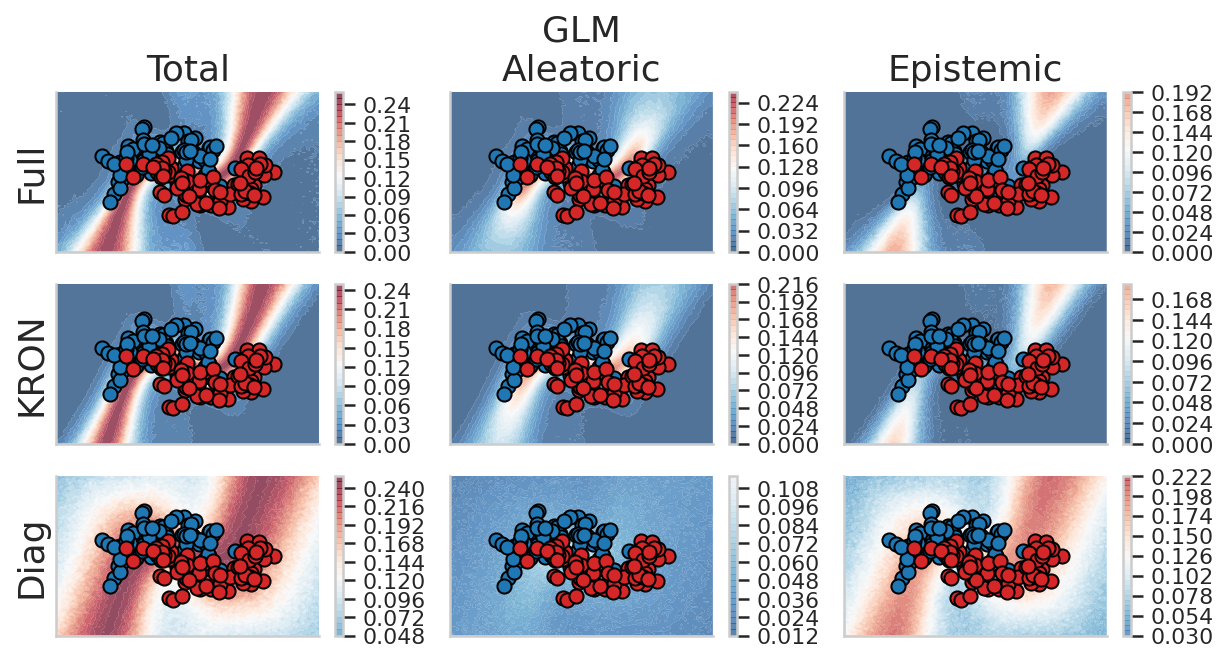
Description we address these issues by attempting to demystify the relationship between approximate inference and optimization approaches through the generalized Gauss–Newton method. Bayesian deep learning yields good results, combining Gauss–Newton with Laplace and Gaussian variational approximation. Both methods compute a Gaussian approximation to the posterior; however, it remains unclear how these methods affect the underlying probabilistic model and the posterior approximation. Both methods allow a rigorous analysis of how a particular model fails and the ability to quantify its uncertainty.
Featured categories
Python (3) Research (3) Bayesian optimization (2)curious about all intersections of data and society.